Revisiting Bayes' Theorem: The Quiet Engine of AI
Bayes’ Theorem is everywhere in machine learning, yet strangely hard to feel intuitively. Even after years in AI and computer vision, I still found it confusing. A centuries-old idea powering today’s models, but never explained in a way that truly clicks. This post is a simple, human walkthrough of Bayes: what it means, why it matters, and how it quietly runs beneath everything we build in modern AI.

1. Why Bayes’ Theorem Feels Confusing?
Let me start with an honest confession: I’ve been in the machine-learning world for years, built computer vision pipelines, deployed models, tuned losses, fought with dataset imbalance… and still found Bayes’ Theorem strangely slippery. Not the formula itself but the intuition.
Because Bayes’ Theorem isn’t just a formula. It’s a worldview. The phillosophy of update your belief with evidence. A mindset for dealing with uncertainty. It sounds simple but the moment numbers start flying around, I used to lose the plot. Took me some time to re-orient my neural network to think from Bayesian perspective.
If if you feel the same, this post is for you. What's covered in the article?
- Bayesian intuition
- A bit of mathematics
- How it connects to modern AI
I have written the post in a way that repeats the terms again and again. This is intentional. By the end, you won’t just know the theorem. You’ll feel what it’s doing.
2. What Bayes’ Theorem Really Says (PLP)
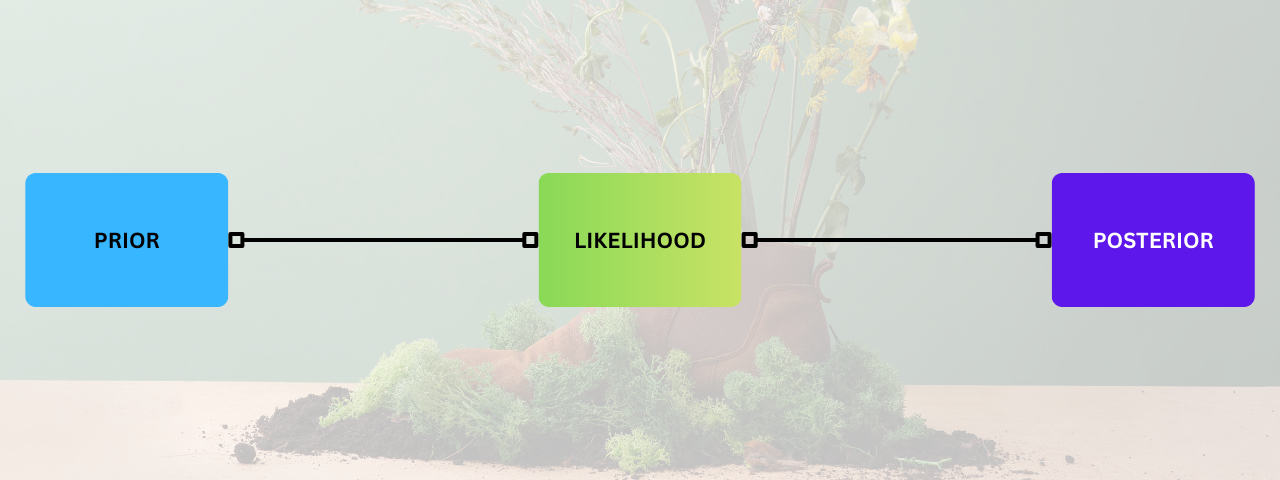
Let’s avoid equations for a moment. It's simply a connection between events and outcomes. I like to remember it as PLP in short.
| Prior | Likelihood | Posterior |
|---|---|---|
| It’s what we think before seeing anything | We see some evidence | We adjust our belief |
| eg. It's not going to rain today | eg. Look outside and see dark clouds | eg. Rain is now more likely |
That’s it. Three steps. Nothing fancy! Thomas Bayes' theorised it based on the following:
- How strong was the initial belief?
- How strong is the new evidence?
- How much should the evidence shift the belief?
The magic lies not in the formula, but in the interaction:
- high prior + strong evidence = very high posterior
- low prior + weak evidence = still low posterior
- low prior + strong evidence = interesting middle ground
- high prior + contradictory evidence = prior drops sharply
- This system mimics how humans revise opinions but much more consistently.
This belief-updating engine is precisely what machine learning systems do. They ingest data (evidence) and adjust parameters (beliefs). Next, we'll look at the mathematical form and connect each term to the intuition above.
3. The Bayes' Theorm Formula Explained
But let’s translate it into English instead of math-speak.
-
: your belief before new evidence (the prior)
-
: how compatible the evidence is with your belief (the likelihood)
-
: your belief after seeing evidence (the posterior)
-
: a normalization factor (it makes sure all probabilities add up to 1)
The entire formula basically says that Posterior = Evidence × Prior, renormalized.
Imagine you’re adjusting a knob. The stronger the evidence supports a hypothesis, the more that knob turns up. The stronger your prior belief was, the less drastic the change will be. A tiny prior requires huge evidence to make a dent. A strong prior can outweigh weak evidence.
This is why a positive medical test doesn’t guarantee disease. If the disease is rare (tiny prior), even strong evidence (accurate test) gets outweighed
4. How Is Bayes Everywhere in Machine Learning?
You can go years without writing Bayes’ theorem once and still be doing Bayesian inference millions of times per second.
When I was working with computer vision initially, I ignored this part as I never had to deal with it. However, even if you never write Bayes’ Theorem in your ML code, you’re using it under the hood. The math may be too complex however they approximate the same idea. Update beliefs (weights) based on evidence (data) through repeated exposure (training epochs). Modern AI is just “Bayesian belief refinement” done millions of times.
Here's where Bayes is hiding in plain sight.
- Training
- Regularization
- Predictions
- Deep Ensembles, MC Dropout, Stochastic Weight Averaging, Adam/ SGD with momentum etc.
4.1 Model Training ( Maximizing Likelihood )
Pure cross-entropy / negative log-likelihood minimization = Maximum Likelihood Estimation (MLE)
This is Bayesian inference with a flat (or implicit uniform) prior. We completely ignore P(θ) and only maximize P(data | θ).
When we add regularization, we turn MLE into Maximum a Posteriori (MAP) estimation. Now we are doing real Bayesian inference!
4.2 Regularization ( Chooseing A Prior Over Weight )
| Regularization | Equivalent Prior on Weights |
|---|---|
| L2 (weight decay) | Gaussian prior centered at 0 |
| L1 | Laplace prior (encourages sparsity) |
| Dropout (at train) | Approximate Bayesian model averaging |
| Label smoothing | Prior that no class is 100% certain |
| Early stopping | Limits effective capacity ==> indirect prior on complexity |
4.3 Predictions (Posterior Probabilities)
Every time a classifier outputs a softmax probability vector, we are reading:
Softmax outputs or calibrated probabilities are literally P(class | input, training data) under the model.
4.4 Few More Connections
Deep ensembles, MC Dropout, SWAG, Laplace approximation etc., explicitly try to approximate the true Bayesian posterior P(θ | data), not just a point estimate.
| Technique | Bayesian Interpretation |
|---|---|
| Deep Ensembles | Poor man’s Bayesian model averaging |
| MC Dropout | Variational approximation to posterior |
| Stochastic Weight Averaging (SWA) | Samples from flatter region ≈ higher posterior density |
| Adam/ SGD with momentum | Approximate natural-gradient in parameter space |
5. Case Study-Naive Bayes: Bayes Theorem in Its Purest Form
Naive Bayes is one of the rare algorithms where the theorem is not hidden at all. It’s the main engine.
The strong assumption is independence between features. That’s why it's “naive”. But this assumption makes it stupidly fast and surprisingly effective. Here’s a tiny working example. The predict_proba output is exactly the posterior probabilities computed using Bayes’ Theorem.
1from sklearn.naive_bayes import GaussianNB
2from sklearn.datasets import load_iris
3
4X, y = load_iris(return_X_y=True)
5model = GaussianNB()
6model.fit(X, y)
7
8print("Predicted class:", model.predict([X[0]]))
9print("Posterior probabilities:", model.predict_proba([X[0]]))6. The Philosophical Angle: What Does It Mean to “Update a Belief”?
This is the part I personally struggled with the most. Not the math, but the meaning. Bayes’ Theorem deals with beliefs, not certainties. Two people with different priors can see the same evidence and come to different conclusions. And that’s not a bug - it’s the entire point.
Let’s break down the philosophy gently.
Probability Is About Uncertainty, Not Randomness
Events aren’t always random, our knowledge is.
- A disease test doesn’t change whether you have a disease.
- A weather forecast doesn’t change whether it will rain.
- A neural network prediction doesn’t change the true label.
Bayes helps you quantify how uncertain you should be.
Beliefs Should Change When Evidence Arrives
The moment we see new data, our mental landscape shifts. If the shift is small, it implies - This evidence isn’t very surprising. On the otherhand, if the shift is big - this evidence forces us to rethink the assumptions. We humans do this all the time - but inconsistently. Bayes does it consistently.
Priors Aren’t Biases, They’re Context
A prior isn’t unfair prejudice; it’s context. Let's look at the following example.
A medical test in a population where a disease is rare should treat positives with caution.
It’s not being biased, it’s being realistic.
In engineering terms it can be put as follows.
prior = background knowledge that prevents hallucinations.
Without priors, you overreact to every piece of weak evidence.
6.1 Why Bayes Feels So Hard Emotionally?
Because it challenges intuition. We’re wired to think linearly:
- test positive ==> must be sick
- cat looks like dog ==> model must be wrong
- one loss spike ==> learning gone wrong
Bayes forces us to think proportionally:
- how strong was my belief
- how strong is this new signal
- how should this signal weigh against everything I know
This proportional thinking is what makes Bayes powerful and mentally demanding.
9. Conclusion: You Don’t Need to Master Bayes to Benefit From It
You don’t need to be a probabilistic wizard. Modern ML systems already use Bayesian principles under the hood. Your job is simply to understand the flow. That’s the core of everything from Naive Bayes to LLMs or VLMs. Bayes’ Theorem is three centuries old, but it still describes exactly how machines (and humans) learn from data.
This post wasn’t about memorizing a formula. It was about seeing the idea behind it. Because once you get that idea, the rest of AI makes a lot more sense.
← Previous Post
ESP32-CAM Smart Doorbell Part 3: With Rock-Solid Reliability
Next Post →
The Kernel Trick in Support Vector Machines (SVMs)
If the article helped you in some way, consider giving it a like. This will mean a lot to me. You can download the code related to the post using the download button below.
If you see any bug, have a question for me, or would like to provide feedback, please drop a comment below.